家长群里人言啧啧suzyq 足交，有说题错了的，也有说题超纲了的，也难怪会杜绝后患！大大齐家长觉得：①此题诞妄，粗略率遗漏了要求“E为AC中点”；②即便已知E为AC中点，此题也超纲，非使用勾股定理不成！

这是一齐某小学六年纪数学竞赛题，原题如下：

图一

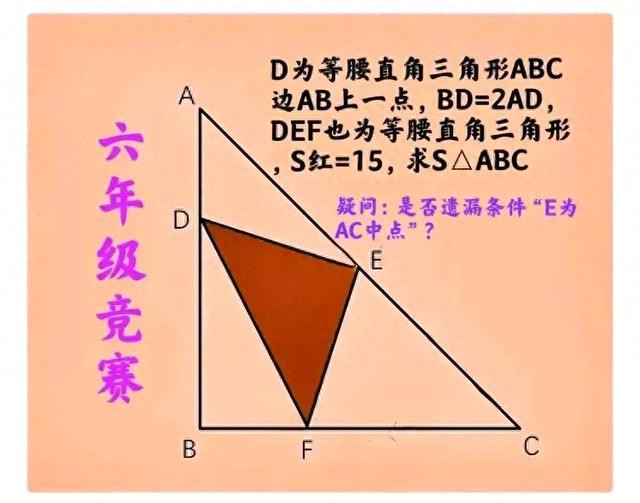
在等腰直角三角形ABC中，BD=2AD，点△DEF亦然等腰直角三角形，S△DEF=15，求三角形ABC的面积。

疑问：此题当真遗漏了要求“E为AC中点”？

一、可证：E为AC中点，但需使用超纲常识！

解说所需常识：①图形旋转+垂线唯独性，或②三角形相通与全等！

①过点E区别作AB和BC的垂线EG和EH，如图二

图二

②持重到∠DEF=∠GEH=90°，西伯利亚属鼠故∠DEG=∠FEH，∠EDG=∠EFH，从而△DEG∽△FEH（相通）。再由DE=EF即知△DEG≌△FEH（全等），进而可得EG=EH。此处超纲！

或②'

将△DEG绕点E逆时针旋转90°至DE与EF重合，旋转后的△DEG记为△FEG'。持重到∠EFG'=∠EDG=∠EFH，故G'必在BC上，由垂线的唯独性即知G'与H重合。也即旋转后的△DEG与FEH重合，从而EG=EH。此处仍有一定超纲嫌疑（定点到定直线垂线的唯独性）！

③四边形BGEH为正方形，吉吉影音制服丝袜畅达BE（如图二），则∠EBG=EBH=45°，从而BE垂直AC，因此E为AC中点。

二、分解：已知E为AC中点情形，仍需使用初中常识勾股定理！

①将△ADF绕点F逆时针旋转90°，则ED与EF重合，点A与点B重合，即△ADF旋转后与△BFE重合，从而AD=BF，BD=CF。如图二

②持重到S△DEF=15，故DF²=4S△DEF=60。

③由勾股定理可得BD²+BF²=DF²，故5BF²=60，也即有AB²=9BF²=108，因此S△ABC=1/2AB²=54！

三、对小学生而言，宜将“E为AC中点”四肢已知要求！

从“一”和“二”来看，若未陈诉E为AC中点，此题难度太大，且使命量也相配大！即即是中学生，能答出来的比例粗略率不会太高！

是故，四肢小学竞赛题，最佳径直陈诉E为AC中点！即便如斯，仍需使用超纲常识勾股定理才调求解！

——————————

友友们suzyq 足交，何如看？接待留言共享！